In an earlier post I explained why '
Ergodicity Economics' is shite. Today I'll dissect a
blog post by its champion, Ole Peters who writes-
Not all academic fields have a clear starting point, a seminal paper that constitutes the foundation of the entire discipline. But economics does. The paper that defines modern formal economics was written by Daniel Bernoulli in 1738.
Bernoulli contributed to probability theory, statistics, and fluid dynamics. He did not contribute to Economics. Indeed, the standard models of Economics which are taught in introductory courses are deterministic and don't feature any type of Uncertainty or turbulence. Moreover, uncertainty in Econ is 'Knightian'- i.e. we don't know the underlying probability distributions or the range of possible states of the world. Failure to account for Knightian Uncertainty- for e.g. by creating what are known as 'Arrow-Debreu' securities- is to create what Warren Buffet is supposed to have called 'Financial Weapons of Mass Destruction'.
Utility theory was introduced by Jeremy Bentham in the Nineteenth Century. Utility is subject to diminishing returns just like farm land- the original paradigmatic example- in that more fertile land is used first and then subsequently less fertile land- called 'marginal' land- is brought into use at higher cost. During the course of the Nineteenth Century, as older 'Marxists' of my vintage will recall, it was discovered that this 'Physiocratic' notion of marginality was wrong. In America there was evidence that marginal land is cultivated first- indeed, a little thought will show this must be the case, while it was only later that very fertile 'bottom' land was drained and brought under the plow. Similarly, when it comes to Utility, there can be 'increasing returns' both individually and socially. There is a hilarious novel by Indra Sinha about a guy who gets addicted to 'call-up' internet chat lines in the early Nineties and goes bust coz his phone bill is through the roof. My memory is, by the time the novel came out, even poor people like me had unlimited 56k dial up internet for a small flat fee. Still, I cancelled my contract after the novelty wore off. But within three or four years we had 'Broadband' sufficient to let me stream my Indian Music and old Bollywood films. Yet it is only now that I could be said to be addicted to the internet. Still, 'diminishing returns' haven't set in coz I watch Netflix while on the exercise machines at the gym and use Spotify while walking or jogging. Indeed, if I knew how to cook, I'd be using the internet to make my curry rather than using it to order shite 'takeaway'.
My point is that 'diminishing returns' was just propaganda. It wasn't something anyone- save some pedagogues and ideologues - took seriously. If they did, the consequences were dire.
To be useful, Utility must be transferable in at least one of its factors. Anything 'hedonic' or otherwise desirable which is wholly unfactorizable such that no transferable element obtains, is outside the scope of Economics. It may be Soteriological or Aesthetic or something wholly apophatic. But, even if it involves choice under scarcity, it isn't Economic but rather 'Akrebic'.
This isn't taught to you in Econ 101- but neither is it taught that you ought not to stick your thumb up your butt and jizz from the lectern. Rather, it is an 'unthought known'.
There have been periods when State power is highly coercive for a fiscal reason- e.g the need to finance War Debt. During such periods it makes sense for 'public intellectuals' to pretend that 'lotteries' offered by the State really are what they claim to be. It would have been unpatriotic, or seditious, to suggest otherwise though it was also 'Common Knowledge' that such was indeed the case. However, this poses no great scandal. Nomos
is Phusis within our species' quite wide margins of survival. What matters is that entry exceeds exit at those margins.
During such periods, there is a 'Straussian' element in Econ writing- i.e. patent absurdities are treated as alethic. At such times, sensible mathematical economists- like Slutsky- pretend not to be mathematical economists at all- he who could have outdone Frank Ramsey!- while some gormless math mavens seek to prove their loyalty, and utility to the High Command, by pretending that Econ is Physics. It isn't. The
'Schweinemord' is an example. If you let Statisticians in the bureaucracy kill off the pigs, coz pigs are 'co-eaters', those stupider than pigshit savants will think gas chambers a swell idea ;-more especially for that most highly productive portion of the population which doesn't even eat pork.
Still, the interessement of math mavens can be a good thing for 'Operations Research', Linear and Dynamic programming, Control Theory and so on. But there is no need for us now to pretend this shite don't stink unless we are actually employed by a Bernie Madoff and can't pay our alimony or keep out of jail any other way.
Expected utility theory is probabilistic and ignores 'Common Knowledge' coz it is either stupid or meretricious. However, because it fails to account for Knightian Uncertainty, it is obvious that its use would be highly mischievous. All this was well known by the time I started studying Econ back in the Seventies.
Peters however thinks Bernoulli invented expected utility theory and that subsequent economists like Smith, Ricardo, Marx etc had heard about him. This is wholly untrue. Bernoulli spoke of the
'emolumentum medium'- or average reward- from a gamble. A poor man would sell a lottery ticket for less than its expected value because he would feel greater regret for not doing so if he failed to win. This is not 'utility maximisation' at all. It is regret minimization. An emolument is not itself utility. I recall a friend of mine who gave up a promising career in Merchant Banking for a low paid admin job with the BBC. Why did she do so? The answer is that her goal was to write scripts and direct TV series. In those days, the Beeb promoted from within. She felt she had been given a once in a life-time opportunity to break out of her bourgeois social class and became part of the Bohemian set. She never did make it in Show Biz, but has no regrets because she felt she'd given herself a fair crack of the whip. We can't say she 'maximised her utility'- she honestly didn't know whether or not she had what it takes to succeed in the field she was attracted to. Interestingly, after marriage, when her kids started school, she went back to work for what was then the Audit Commission. I imagine she did very well when she joined the Private Sector. Thus, in the end, she probably did maximize her emoluments!
Economists with a literary bent are aware of the Epicurean School of Economics whose most famous exponent was Philodemus of Gadara whose verses were praised by Cicero for their elegant lasciviousness. 'Emolumentum' is a rather Ciceronian word. The point Cicero was making (in his diatribe against Caesar's father-in-law) was that a coarse type of hedonism defeated its own purpose. It provoked disgust. It maximised regret. To have over-eaten at a banquet where only the choicest viands were on offer is one thing. It is quite another to gorge yourself out of a restaurant garbage pail despite being as rich as Croesus.
Bernoulli, however, was not an Epicurean but, rather, addressing a current question which was essentially about explicating probability theory so it could be used in Physics and Actuarial Science and other such useful avocations. He was not looking at real world 'chrematistics' (i.e. wealth generating strategies) and thus was neglecting arbitrage on the basis of 'Common Knowledge' (this yields what is known as 'Muth Rationality' and gets rid of 'path dependence', thus establishing ergodicity).
Bernoulli says
'Until now scientists have usually rested their hypothesis on the assumption that all gains must be evaluated exclusively in terms of themselves, i.e.,
on the basis of their intrinsic qualities, and that these gains will always produce
a utility directly proportionate to the gain.' This is true enough. I'm a very poor man. Suppose I suddenly get a lottery ticket which pays out 20,000 ducats or nothing with equal probability. What do I do? The answer is I approach rivalrous arbitrageurs and ask them to quote their 'spread' for the ticket. I use an optimal stopping rule- like in the Secretary problem. So, if I find the first three brokers quote pretty much the same spread, I chose the one I like and sell my ticket. The more 'open' and frictionless the market, the closer my 'emolumentum' is to the Expected value of the lottery.
Bernoulli was assuming 'fair games'- i.e. frictionless ones- and this is genuinely useful in some applications of math having to do with 'games against nature'. But
chrematistic games don't have this quality because humans exhibit mimetic effects and have Schelling focal Common Knowledge type correlated equilibria. However, because of Knightian Uncertainty, they hedge on- even ontologically dysphoric- discoordination games. Thus General Equilibria are 'anything goes' which also explains why your and my life is so much less utterly shit than that of our ancestors.
Bernoulli says- '
Any gain must
be added to the fortune previously possessed, then this sum must be raised to the power
given by the number of possible ways in which the gain may be obtained; these terms
should then be multiplied together. Then of this product a root must be extracted the
degree of which is given by the number of all possible cases, and finally the value
of the initial possessions must be subtracted therefrom; what then remains indicates
the value of the risky proposition in question. This principle is essential for the
measurement of the value of risky propositions in various cases.'
This is obvious nonsense. Gains can be given away or used to purchase some wholly different type of psychic benefit- e.g. public esteem, political power and so forth. What matters is if arbitrageurs exist between 'coordination' and 'discoordination' games. But why shouldn't they? Bernoulli lived in a Society where Wealth could turn into Nobility- or even Royalty- while Poverty caused loss of caste. Petronius' Trimalchio could be a Maecenas if he had better taste. But, by purchasing a sufficiency of Greek slaves, he could ensure that his heir had the right type of Paideia.
Ole Peters, being impartially ignorant of both Bernoulli's and our own epistemic
mise en scene, says that Bernoulli-
introduces expected utility theory.
Surely, Bernoulli is invoking some sort of notion of diminishing returns to challenge what he believed to be the prevailing hedonic calculus? Yet, if there is Common Knowledge and arbitrage is more or less frictionless, then the Expected Values
is the 'emolumentum medium'.
Not content with telling a stupid lie, Ole Peters makes an even more ludicrous claim-
The main thrust of our work is, of course, to replace expected utility theory and instead work with time-average growth rates of wealth.
Nobody knows what is or isn't wealth. Only time will tell if an asset really is productive or if it is a white elephant. Only God knows the 'time-average growth rates of wealth'. There may be expectations of what they might be but those expectations are known to be
a priori wrong because 'wealth' is defined in terms of 'income' and vice versa, with both being known- because Death exists at both the individual and the species level- to be radically uncertain and thus fundamentally unknowable save after the fact.
The 'time-average' growth rate of wealth of a Miser or a Midas or a Thief may appear high. But those fuckers die sooner rather than later and, guess what?, can't take their ill gotten gelt with them. Who doesn't know this? Only good ol' Ole Peters. What is he drinking?
- I’ll mention how that works, but the focus of this post will be on something else. Bernoulli’s paper is not only conceptually misleading but also technically flawed in a sneaky way that keeps confusing everyone. Where Bernoulli determines the price to be paid for a risky prospect, he contradicts himself. I wouldn’t make such a fuss about this if the paper wasn’t so absolutely crucial. This basis of economics contains an error that invalidates commonly held beliefs and puts tens of thousands of studies into a different light. I recently encouraged people, using twitter, to read the paper and see for themselves. In this blog post I go through the relevant analysis step by step and address questions that came up in response to the tweet.
Nobody read Bernoulli's paper. Nor did they read Karl Menger- coz it was his Dad who was the economist. The guy was a refugee from a shithole country who burbled shite about 'meta-economics' at a time when it was already clear that the most economical use of mathematical economists was to plug them into the most boring and tedious type of O.R coz, at best, they are a superior type of Accountant.
Still Menger's Math was good. His 'Super Petersburg paradox' is interesting because it features types of functions whose growth rates can overtake each other in non obvious way. This is useful heuristically. But, it is silly. We know that a Lottery which raises the cash prize at a faster rate than we lose interest in it is a con. Still Menger has a place in the history of mathematical economics. Sadly, mathematical economics has a place in the history of economics only as the butt of ridicule coz it shat the bed everywhere it gained currency.
Bernoulli's own view was that gambling was foolish.
'First, it appears that in many games, even those that are absolutely fair,
both of the players may expect to suffer a loss; indeed this is Nature's admonition to avoid the dice altogether' However, he gave the wrong explanation for it. Replace the words 'game' and 'dice' with 'risk pooling' and 'insurance scheme' respectively and Nature's admonition would be to take even somewhat 'unfair' offers so as to create a Social Insurance safety net. This does not depend on 'cardinal utility' or 'interpersonal comparisons' or even the diminishing marginal utility of money. It is the Hannan Consistent strategy.
It is useful for Math mavens to look at the growth rate of different types of functions but such functions don't appear in Econ. That's why mathematical economists aren't running things.
Bernoulli’s paper was re-published in 1954 in Econometrica (if you don’t like paywalls, here’s a free pdf). This is the standard translation from Latin, and page numbers below refer to it. I have not read the original Latin paper, but the error is spelled out in words, visually in a figure, and also in an equation, so this is not something lost in translation. If you have a copy of the original, please send it to me. [2018-02-18 addendum: a scan of the original is here.] The paper is so fundamental to economics that more than 200 years after its publication it was fished out of the proceedings of the Papers of the Imperial Academy of Sciences in Petersburg (Vol. V, 1738, pp. 175-192), translated into English, and published in the leading journal of the field.
If it was fundamental to econ, how come no economists knew about it? Why did it have to be fished out from some archive in the Soviet Union? Back in '54, few economists read Econometrica because they didn't have the mathematical chops. It wasn't till the next decade that Harvard dropped the foreign language requirement, substituting a math requirement, for a PhD in Econ. This was a good thing coz reading German makes you stupid and evil. Doing a bit of Math just makes you a conceited prick whom any teenager can intellectually kick in the goolies coz that's how Maths works. It weeds out utter shitheads.
- Expected utility theory (EUT) is a form of decision theory. Imagine someone offers you a lottery ticket. Prior to Bernoulli, it was assumed that people roughly maximize the expected change in wealth resulting from such a gamble. That is, if initial wealth is
 and possible changes in wealth are
and possible changes in wealth are  then you’d maximize
then you’d maximize
- (Eq.1)
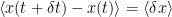 .
.
Would you buy a lottery ticket off me? No. You'd suspect it was a scam. Indeed, sensible people don't buy lottery tickets because they are a 'tax on stupidity'.
Before and after Bernoulli, nobody bothered greatly with gambling- except gamblers. Casinos welcome punters who have devised full-proof systems to win at roulette. One may as well try and patent a permanent motion machine.
The way you maximize your wealth is not by gambling but by keeping abreast of new developments in your field and investing in promising ventures which, unlike gambling, involve 'positive sum' games- i.e. increase aggregate output.
Consider what Bernoulli himself said re. 'positive sum' games in the paper Ole Peter's relies on- .'
The procedure customarily employed by merchants in the insurance of
commodities transported by sea seems to merit special attention. This may again
be explained by an example. Suppose Caius, a Petersburg merchant, has purchased commodities in Amsterdam which he could sell for ten thousand rubles
if he had them in Petersburg. He therefore orders them to be shipped there by
sea, but is in doubt whether or not to insure them. He is well aware of the fact
that at this time of year of one hundred ships which sail from Amsterdam to
Petersburg, five are usually lost. However, there is no insurance available below
the price of eight hundred rubles a cargo, an amount which he considers outrageously high. The question is, therefore, how much wealth must Caius possess
apart from the goods under consideration in order that it be sensible for him to
abstain from insuring them?
This is a stupid question. If insurance premiums are indeed 'outrageously high'- i.e. yield economic rent- then there is an arbitrage opportunity. Make money of that by forming a coalition which 'internalizes externalities' and overcomes information asymmetry.
Suppose this is not possible because of the backwardness of your locale. Still, some people with little wealth should take the gamble while some with much wealth should not. Why? Because of hysteresis of a 'charismatic' sort. Venture Capitalists, following portfolio choice theory, do in fact finance young 'outsiders' who take this sort of gamble and end up hammered on 'Change. Consider what happens when Baron Rothschild takes a gamble of this sort and wins. Nobody cares. Big yawn. But if Baron Rothschild takes up the guttersnipe Schlemiel ben Schlemazel and
he wins big time- then new horizons are opened up- not all purely chrematistic.
We live in a world- or at least Indians do- where Angel Investors can get a higher tax liability for doing precisely this type of arbitrage.
Bernoulli writes from the perspective of the Roman Law which defined 'culpa levis in abstracto'- or negligence with respect to the highest standard of care and diligence- with respect to the 'bonus paterfamilias'- the ideal patriarch, perhaps of Senatorial rank, with a very thorough knowledge of the world, who exercises a sort of trusteeship on behalf of his wards.
The problem here is that even by Cicero's time, financial markets had moved forward on the basis of 'Common Knowledge' type Muth Rationality. In other words, this math maven was babbling nonsense with respect to the commerce of his own time.
If x represents his fortune, then this together with
the value of the expectation of the safe arrival of his goods is given by
10(X + 101)95X5 (X + 00)'9x in case he abstains. With insurance
he will have a certain fortune of x + 9200. Equating these two magnitudes we
get: (x + 10000)19x = (x + 9200)20 or, approximately, x = 5043. If, therefore,
Caius, apart from the expectation of receiving his commodities, possesses an
amount greater than 5043 rubles he will be right in not buying insurance. If,
on the contrary, his wealth is less than this amount he should insure his cargo.
And if the question be asked "What minimum fortune should be possessed by
the man who offers to provide this insurance in order for him to be rational in
doing so?" We must answer thus: let y be his fortune, then
20 ~ ~ ~ = 2A/(y + 800)19. (y -9200)=y
or approximately, y = 14243, a figure which is obtained from the foregoing
without additional calculation. A man less wealthy than this would be foolish
to provide the surety, but it makes sense for a wealthier man to do so.
Nonsense! This is an arbitrage opportunity. You trade off the credibility of the surety provider against his Shapley value- i.e. you shift risk to the shoulder least able to bear it and thus with the lowest leverage in getting a bigger slice of the pie. No doubt, this may be a 'bargaining problem' rather than incomplete adhesion contract, but, if it is, the counterparty can do a deal with you to offload risk onto
their more stupid counterparties. It is these sorts of processes- some mimetic, some Common Knowledge & 'Muth Rationality' based- which have permitted language to flourish as the solution to both coordination and discoordination problems. Commerce is merely a prescriptive type of language. Sure, it has a mathematical representation but only in a univalent foundations, type theoretic, protocol bound and therefore non canonical form.
Bernoulli says-
From
this it is clear that the introduction of this sort of insurance has been so useful
since it offers advantages to all persons concerned. Similarly, had Caius been
able to obtain the insurance for six hundred rubles he would have been unwise
to refuse it if he possessed less than 20478 rubles, but he would have acted much
too cautiously had he insured his commodities at this rate when his fortune was
greater than this amount. On the other hand a man would act unadvisedly if
he were to offer to sponsor this insurance for six hundred rubles when he himself
possesses less than 29878 rubles. However, he would be well advised to do so if
he possessed more than that amount. But no one, however rich, would be managing his affairs properly if he individually undertook the insurance for less than
five hundred rubles.
Any actual businessman could explain Bernoulli's error. Arbitrage is ubiquitous. All Enterprises are 'discovery processes'. If you find out there is an economic rent in an area you would otherwise access, form a coalition to enter that field. This is not 'Tarden mimetics'. It is Muth Rational behaviour and the reason we as a species remain unified.
Ole Peters does not understand that, for Human beings, Expectations are 'crowd sourced'. Provided arbitrage is permitted, Bernoulli & Menger & Von Neumann & Morgenstern & Arrow etc were just talking worthless shite. But everybody already knew that by the time I was in short pants and the Sonnenschien-Mantel-Debreu theorem percolated into Mathematical Econ 101. Actual Econ, didn't need it, coz it wasn't utterly shite from the get go.
- Here,
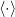 is the expectation operator. Some people like to denote it by
is the expectation operator. Some people like to denote it by  but it’s same thing. If
but it’s same thing. If 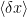 is positive, you’d buy the ticket, if it’s negative, you wouldn’t. But observations soon convinced everyone that this is not how people behave.
is positive, you’d buy the ticket, if it’s negative, you wouldn’t. But observations soon convinced everyone that this is not how people behave.
If it were positive, the guy running the lottery will go bust. He won't be able to pay out. One may as well give Bernie Madoff your money.
This doesn't mean it is irrational to 'have a flutter' once in a way. But your bet is so small it makes no real difference. We say there is a psychic benefit- some 'utility' is gained by doing something irrational just for the thrill of it.
- EUT was introduced as a refinement of this decision criterion. It says that you will choose the action that maximizes the expected change, not of your wealth but of your utility. The insight here is that people don’t evaluate gambles in isolation but with respect to a reference level (their initial wealth). An extra dollar is worth less to me if I’m rich than if I’m poor. Mathematically, a so-called utility function
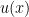 is introduced, where
is introduced, where  represents wealth.
represents wealth.
This is silly. Gambling has nothing to do with Economising. Sure, buying a raffle ticket once in a way may be fun but don't make a habit of it. True, a very rich man may gain more pleasure from gambling because he is the center of attention and, even if he loses, it won't make much difference to him. By contrast, the guy who is betting his last dollar is trembling with fear and may leave the table to go blow his brains out in the alley way.
- The most commonly used utility function is
 . This is motivated by assuming that the extra utility someone attaches to an extra dollar is inversely proportional to the wealth that that someone already has,
. This is motivated by assuming that the extra utility someone attaches to an extra dollar is inversely proportional to the wealth that that someone already has,
The reason I wasn't taught this was because the thing was patently absurd. Utility has no relationship at all to wealth. It does relate to Consumption but, long term, that Consumption has to be sustainable- i.e. it shouldn't cut into one's Wealth (which is defined as the set of assets needed to generate a given level of Income. Deduct 'depreciation' of assets and you have 'Net Income'. If you want to better off in the future- or if you know a time will come when you can no longer work because you are too old or have fallen ill- then you should save and invest out of your current Income. But, you should not go to an extreme and starve yourself to death so as to hoard assets.

The 'unusual' means that which was not predicted. But man has evolved on a highly uncertain fitness landscape. Rather than gambling, one should find 'structural causal models' which don't just predict things better, thus reducing Risk, but also enable one to actually change how things are made so that everyone can have more for less effort.
Still, I suppose,
historians of Economics can say 'Bernoulli anticipated the theory of diminishing marginal utility'. But such historians don't greatly matter. Nobody, but a couple of senile pedagogues, cares who has precedence in formulating a doctrine which is merely common sense.
- Later on Bernoulli writes this assumption as the differential equation
 , whose solution is the logarithm. Let’s write down what EUT wants us to maximize:
, whose solution is the logarithm. Let’s write down what EUT wants us to maximize:
- (Eq.2)
 .
.
This is a silly equation. Capitalists don't stop being capitalists just because they are at the satiation point for Utility. Why? Money is 'transferable utility'. They can make more money and give it away and get a reputational benefit. Alternatively, they can advance Science or the Arts or their own political agenda. This equation is quite worthless.
- What’s our conceptual critique?
- By re-writing this object you will immediately see that it actually means something else, and that’s the essence of our conceptual critique. Logarithms turn division into subtraction,
 . So (Eq.2) can be re-written as
. So (Eq.2) can be re-written as
- (Eq.3)
 .
.
- Now divide both sides by

Why bother? It is 1. It leaves the equation wholly unaltered.
- (Eq.4)
 .
.
- What’s this? In any field other than economics, this object is called the expected exponential growth rate of wealth.
That's true of the right hand side of the equation. The left hand side says that Utility is equal to it which is a foolish assumption.
- No utility required, no psychology required.
The assumption that utility depends on wealth is psychological.
- Digging just a little bit deeper, the whole story comes to light. Wealth dynamics are fundamentally multiplicative — we can invest wealth to generate more wealth.
We can also invest wealth and find we pissed it against a wall. The dynamics of Wealth are regulated by Economic constraints of a physical, not notional, type.
- For such dynamics the exponential growth rate is an ergodic observable, which means its expectation value tells us what happens in the long run.
Sadly, it is a difficult matter to tell a Bernie Madoff from a Warren Buffet. On paper, a fraudster's scheme may look more promising than that of a genuine Wall street wizard. 'Ergodic observables' are horseshit. We won't back the fraudster if we find out, after Googling him, that he has been accused of running scams in other towns. We will back the wizard when, like Buffet, he has a great track record and is a genuine philanthropist. 'Path dependence' matters- the fraudster's past tells us something about his future. Ergodics- i.e. the notion that the past does not matter- is just what con-men rely on to convince you they have turned over a new leaf and this time they really have found the formula to extract gold from horseshit.
- Mystery solved! People just optimize what happens to their wealth over time. Crucially, additive wealth changes,
 are not ergodic, wherefore the expectation value in (Eq.1) does NOT tell us what happens over time.
are not ergodic, wherefore the expectation value in (Eq.1) does NOT tell us what happens over time.
Either wealth changes or it does not. If this is determined exogenously, then ergodicity obtains. If not, then it doesn't even if you take the log of a ratio instead of the ratio itself. Thus, suppose all fund managers are equally smart and equally honest and the only thing which determines their success is exogenous factors- e.g. commodity prices, geopolitical factors etc- then expectations are ergodic. However, if some are crooks and others are honest and smart, then 'hysteresis'- i.e. path dependence will feature.
Only time will tell what happens over time because Knightian uncertainty obtains. This severely limits the application of math to Econ. Moreover, people who study Econ rather than Physics or Computer Science or Biology or whatever, end up working for those who find commercial applications for the things the Scientists and Artists and Chefs and Hairdressers discover. Economists are glorified Accountants and rank below Actuaries. Still, they can do some useful donkey work. But only if they ignore their textbooks and the dreary 'papers' published by pedagogues.
- Economics textbooks and papers miss this point. The problem is treated in an a-temporal space, as a so-called “one-shot game”. The mathematics is the mathematics of things happening in parallel universes, not of things happening over time.
No. The maths is the maths of a 'steady state' equilibrium of a Nineteenth Century type. It has nothing to do with 'parallel universes'. But, it is merely a pedagogic or ideological tool with little practical import.
- Where time is mentioned, it is usually wrongly assumed that
 indicates what happens over time.
indicates what happens over time.
No. The assumption is that it is the end state. The transition may be instantaneous, nevertheless these models are called 'one-period' economies.
- Endless arguments ensue over whether
 is the correct psychological re-weighting people apply to wealth — in reality this is a question about dynamics, with psychology as a second-order effect — of course we can be deceived, confused, or stupid and not act in our best interest.
is the correct psychological re-weighting people apply to wealth — in reality this is a question about dynamics, with psychology as a second-order effect — of course we can be deceived, confused, or stupid and not act in our best interest.
I've known economists all my life. There has never been any such argument even among pedagogues of the obtusest sort. It is obvious that Utility is a function, not of Wealth, but Consumption.
- It’s also far from easy to put a number on wealth
 , or indeed on the different
, or indeed on the different  and their probabilities involved in real-world decisions.
and their probabilities involved in real-world decisions.
It is impossible to do so save after the event. Nevertheless, precisely because of hysteresis, it can be quite useful to do so.
- The history of economics is a wonderful example of how a basic conceptual error prevents the detection of technical errors and inconsistencies.
There was no 'conceptual error'. The history of economics is the history of politics on the one hand and administration on the other. It has absolutely nothing to do with mathematics.
- Without the right concepts it’s just not possible to ask the right questions, let alone find consistent answers.
The right questions to ask are the one's whose answers prove useful. One does not need to have right concepts to start off with. Rather, right concepts arise out of looking at existing 'Structural Causal Models' and tinkering with them till they give superior outcomes. Understanding why the improvement has occurred represents concept formation. The 'right concept' is the one which allows the innovation to spread most rapidly and at the lowest cognitive cost.
- How much would I pay for a lottery ticket?
Just as much as can be justified by the thrill of buying it. But, since lotteries must be negative sum games, don't think of this as an investment or a wealth management strategy.
- Let’s put our conceptual troubles aside for a moment and use EUT to address precisely one of the questions Bernoulli asked. My initial wealth is
 , I have to pay a ticket fee
, I have to pay a ticket fee 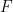 , and I can win prizes
, and I can win prizes  with probabilities
with probabilities  , where
, where  is a random integer denoting which of the
is a random integer denoting which of the 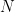 possible prizes I win. We imagine the lottery to take a time
possible prizes I win. We imagine the lottery to take a time  that doesn’t depend on which prize is won.
that doesn’t depend on which prize is won.
Voltaire won a lottery which made him financially secure. But a Society which thinks lotteries are about Wealth Creation is one headed in a tumbril for the guillotine
- EUT says: find the value
 that makes the expected change in utility zero. If I pay more, the lottery will have a negative expected utility change, and EUT would advise me not to take part. Mathematically, here is the object we have to compute:
that makes the expected change in utility zero. If I pay more, the lottery will have a negative expected utility change, and EUT would advise me not to take part. Mathematically, here is the object we have to compute:
- (Eq.5)

- That’s it. Now vary
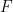 so that the expected change in utility becomes zero. The value of
so that the expected change in utility becomes zero. The value of 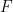 where that happens is the maximum fee I should pay for the lottery.
where that happens is the maximum fee I should pay for the lottery.
- Bernoulli’s error
- Bernoulli makes an error when he talks about this fee. The key figure is on p.26, and I’ve scribbled in red a translation of Bernoulli’s notation into the symbols used in Peters and Gell-Mann (2016).
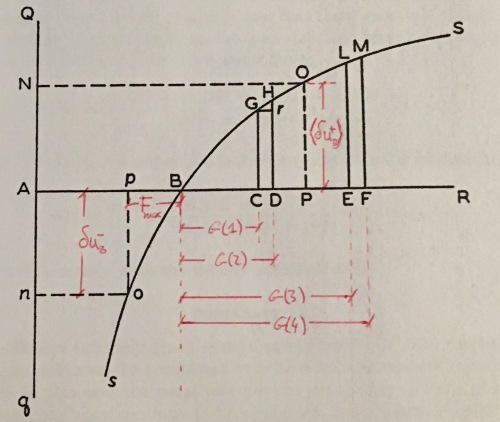
- Let me talk you through the figure. The horizontal axis represents wealth
 , and the vertical axis represents utility, so that the solid curve is the utility function
, and the vertical axis represents utility, so that the solid curve is the utility function 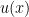 .
.
- Let’s focus on the solid horizontal line first. The point B is the initial wealth
 . The point p, to the left of B, represents the wealth
. The point p, to the left of B, represents the wealth 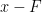 , that is, the initial wealth minus the ticket fee. The points C, D, E, F are wealth levels arrived at by adding to the initial wealth one of the possible prizes
, that is, the initial wealth minus the ticket fee. The points C, D, E, F are wealth levels arrived at by adding to the initial wealth one of the possible prizes  .
.
- You may already suspect the problem: let’s imagine outcome 1 occurs in the lottery, meaning we receive the prize
 . In that case, our wealth will change to
. In that case, our wealth will change to  , and not
, and not  (which is the position of point C). We have to subtract the fee! The points C, D, E, F marked by Bernoulli have no relevance to the problem (unless the fee is zero).
(which is the position of point C). We have to subtract the fee! The points C, D, E, F marked by Bernoulli have no relevance to the problem (unless the fee is zero).
It may be that, at the time, your stake was returned along with your winnings.
- Now let’s walk along the utility curve. The point o marks the utility of wealth
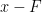 , so that the dashed line po is the drop in utility associated with a drop in wealth from
, so that the dashed line po is the drop in utility associated with a drop in wealth from  to
to 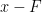 . The points G, H, L, M (to the right of B along the utility curve) represent the utilities associated with the irrelevant wealth levels
. The points G, H, L, M (to the right of B along the utility curve) represent the utilities associated with the irrelevant wealth levels  . The point O represents the expected utility assuming prizes are received with their respective probabilities but no fee is paid, p.26
. The point O represents the expected utility assuming prizes are received with their respective probabilities but no fee is paid, p.26

- In Peters and Gell-Mann (2016) we call this object
 , for want of a better symbol.
, for want of a better symbol.
- Now comes Bernoulli’s error. He claims that the lottery is to be valued by comparing
 to the loss in utility one would suffer if one were to buy the lottery ticket for its fee but not receive any prize. The key passage is on p.26–27
to the loss in utility one would suffer if one were to buy the lottery ticket for its fee but not receive any prize. The key passage is on p.26–27


- This amounts to a decision criterion, different from (Eq.5) and inconsistent with EUT. We denote with the symbol
 what Bernoulli calls “the disutility to be suffered by losing” (Bp in his notation). Now we can write Bernoulli’s decision criterion in symbols. Bernoulli tells us to buy a ticket if the following quantity is positive, and not to buy it if it’s negative
what Bernoulli calls “the disutility to be suffered by losing” (Bp in his notation). Now we can write Bernoulli’s decision criterion in symbols. Bernoulli tells us to buy a ticket if the following quantity is positive, and not to buy it if it’s negative
- (Eq.6)
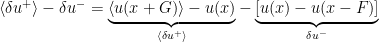 .
.
So Bernoulli is gesturing at the common sense view that, for prudential reasons, a fall in wealth is more greatly feared than a gain is valued. So this is mere 'risk aversion' which was old hat by the time I got to College. Indeed, Econ could have abandoned Utility maximizing models for 'Hannan Consistent' type 'regret minimizing models' but it wasn't worth the bother because the thing was just a pedagogic exercise. It was already obvious that 'Decision theory' was silly. Mechanism Design was the way to go.
- Error or different model?
- In principle, one could now say that Bernoulli just had a different model of people’s behavior than does modern economics. That would be bad enough because modern economics claims that it has the same model as Bernoulli.
Why would it make any such claim? Nobody gives a shit about some dude who died a long time ago.
- It’s more likely that Bernoulli got confused specifically when he tried to find the maximum fee. Otherwise he seems consistent with EUT, for instance on p.24, where he describes the certain profit (“the value of the risk in question”) that corresponds to an uncertain profit

It may be that back in the Eighteenth Century, this type of Rational Analysis was something new. My understanding is that the education of young people destined for commercial careers was changing at this time. Moreover, Governments were becoming more active in developing 'Political Arithmetic' so as to expand their fiscal base and mobilize resources. However, it is scarcely earthshaking stuff. Smart businessmen had been evaluating risk successfully for millennia.
- Let’s really kill this. Why is (Eq.6) not a good decision criterion?
It's coz lotteries don't matter. Buy a ticket from time to time if it gives you a thrill. But don't fool yourself you are doing 'Wealth Management'.
- It is easy to construct an example where the maximum fee I should pay,
 , is smaller than the smallest possible prize in the lottery, but the criterion still tells me to refrain from buying a ticket. That makes no sense: such a lottery has no downside risk. I’m guaranteed a positive net profit, the only uncertain element is how much better off I will be after the game. Intriguingly — have another look at the figure — the maximum fee calculated by Bernoulli is smaller than the smallest possible prize, assuming that one of the prizes will be won (the distance between B and p is smaller than the distance between B and C).
, is smaller than the smallest possible prize in the lottery, but the criterion still tells me to refrain from buying a ticket. That makes no sense: such a lottery has no downside risk. I’m guaranteed a positive net profit, the only uncertain element is how much better off I will be after the game. Intriguingly — have another look at the figure — the maximum fee calculated by Bernoulli is smaller than the smallest possible prize, assuming that one of the prizes will be won (the distance between B and p is smaller than the distance between B and C).
Suppose you email Ole Peters and offer him a chance to buy a ticket in a lottery for 100,000 pounds sterling. The smallest prize is one million pounds. Every ticket is guaranteed to win a prize. The largest prize is ten zillion pounds. Will Peters take it? No. He is only pretending to be stupid. Similarly, he won't queue up to by a lottery ticket costing one penny which pays out two pennies and which only permits one ticket to be sold to each customer. Why? The game is not worth the candle.
Any lottery with a positive Expected Value will crash immediately unless it stipulates only one ticket per customer and the prize is nugatory.
- Another problem is this: how much should I be willing to pay for one dollar, according to Bernoulli? What? … for one dollar? One dollar, of course! Yes, but not according to Bernoulli. Try it out:
 for any non-zero number of dollars I buy in dollars, due to the concavity of the utility function. Therefore, Bernoulli’s criterion tells me that no amount of money is worth that amount of money. Come on! That’s nonsense!
for any non-zero number of dollars I buy in dollars, due to the concavity of the utility function. Therefore, Bernoulli’s criterion tells me that no amount of money is worth that amount of money. Come on! That’s nonsense!
Is it though? Suppose I put an ad in the papers offering two dollars for every dollar mailed to me. By the time I'm arrested I'd have collected only a few hundred dollars because the vast majority of people aren't utterly stupid.
- Bernoulli in practice
- Later, on p.33, Bernoulli works through the specific case of the St. Petersburg lottery. This lottery is defined by
 and
and 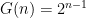 , with
, with  any positive integer.
any positive integer.
The point about the St. Petersburg lottery is it shows that 'chrematistics' (the science of wealth) is as foolish as everybody from the time of Aristotle had said it was. Wealth can go to infinity though Output can't in the same way that Alchemy can turn lead into gold but Chemistry can't.
- But his method is so nonsensical that he does something really curious. He wants to evaluate his criterion (Eq.6) but realizes that that’s cumbersome. He then says that if wealth is very large and the utility function can be considered linear, his criterion can be approximated by (Eq.5), meaning actual EUT. So he uses actual EUT as an approximation:

- Bernoulli’s notation is different from ours (
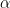 is initial wealth (whereas we use
is initial wealth (whereas we use  ) and
) and  is the fee (whereas we use
is the fee (whereas we use 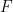 )). Let’s put this back into our notation and show that he really is using criterion (Eq.5) and not his own criterion (Eq.6).
)). Let’s put this back into our notation and show that he really is using criterion (Eq.5) and not his own criterion (Eq.6).
- (Eq.7)

- …take the logarithm
- (Eq.8)
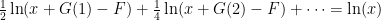
- …simplify…
- (Eq.9)

- …simplify even more and subtract
 …
…
- (Eq.10)
 .
.
- This sets the expected change in logarithmic utility to zero, to determine the maximum fee I should pay, as required by EUT. Bernoulli does not use his own criterion (Eq.6) but the generally accepted criterion (Eq.5).
- Depending on which part of Bernoulli we read, and how carefully we read it, we will come away with a different impression of what utility means and what EUT is. Not surprisingly, the economics literature is littered with arguments and disagreements and invalid studies that seem to arise from a confused use of EUT.
These equations of Peters are as nonsensical as anything in Bernoulli. But the latter did make some great discoveries. Peters can make no such claim. So what if there is some obscure branch of pedagogy in which stupid pedants have silly arguments? Actual economists- and most of us are economists in the sense that we manage our own money- don't bother with some obsolete
methodenstreit which has no relevance to our lives. What we do care out is 'Mechanism Design'- the guys who manage our pension funds should be punished, not rewarded, if they piss our saving against the wall. We need 'incentive compatibility' in financial markets. The 'Rocket Scientists' with their lying 'Li Equations' need a dose of reality. Maybe telling them about 'regret minimization' and Hannan Consistency will help. But, equally, some degree of volatility or turbulent 'noise' is probably needful and desirable for the robustness of the system.
- Serious consequences
- This is a blog post, so let me speculate about the sort of trouble Bernoulli has caused over the centuries.
How can a paper which nobody has read, and which was pretty crap to begin with, have caused any trouble?
- There are special conditions under which criteria (Eq.5) and (Eq.6) are identical. Assuming that they are identical in general (which is often — wrongly — done), one would implicitly assume such conditions. I’ll tell you about two cases with troubling consequences (there are more).
- The fee is zero
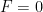 .
.
- Check this for yourself: set
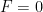 in (Eq.5) and (Eq.6). They really are the same then. But that’s not a very interesting case: of course I should “buy” the ticket if it doesn’t cost anything. Why not?
in (Eq.5) and (Eq.6). They really are the same then. But that’s not a very interesting case: of course I should “buy” the ticket if it doesn’t cost anything. Why not?
If its price is zero it is because there is no demand for it. It is not scarce. My e-books are an example of a good which has a zero price. You could read them for free. Maybe you will enjoy them. But you won't bother because there must be a reason why no one else is reading them.
Dog turds are another example of free goods. You are welcome to pick them up and put them in your pocket. You may believe they will one day become very valuable. But other people are likely to think you are a loony and give you a wide berth.
- The hidden assumption of zero fee utterly confused Karl Menger, and he concluded wrongly that utility functions have to be bounded to treat St. Petersburg-like lotteries.
If a utility function is unbounded, this means there can be a person who can himself be and can himself everybody else infinitely happy. In that case, there would be no scarcity and thus no Economics.
- Samuelson (1977) was so convinced by Menger’s incorrect argument that he wrote “Menger 1934 is a modern classic that stands above all criticism.”
Who now thinks Samuelson was a smart dude? He thought the Soviets might overtake America in terms of material prosperity. Why the fuck was he so obsessed with ordinal utility? Every ordinal measure must correspond to a cardinal measure. Why treat the latter as the Devil?
- Menger’s study (in German and behind a paywall) is here.An English translation (careful, it has a few typos) is in this book:
- Menger (1967) The role of uncertainty in economics. English translation by W. Schoellkopf and W. G. Mellon. In: M. Shubik (ed) Essays in mathematical economics in honor of Oskar Morgenstern, Princeton University Press, Chap. 16, pp 211–231).
- I have discussed the problem here.
In the relevant paper, Peters wrote-
In his Section 2, on p. 212, Menger wrote, referring to the original game A: “If
B, who has an infinitely large expectation, would be willing to pay any amount of
money for the privilege of playing the game, then this behavior would conform to his
infinitely large mathematical expectation [...]
Actually B shouldn't have an 'infinitely large expectation' because infinite wealth is not feasible.
Not only will B not pay an infinitely
high price to play the game, since this is impossible, buy he will not pay a very high
price that he could afford. In any case, he will not, if he is sane, risk all or even a
considerable portion of his wealth in a Petersburg game.”
This is common sense. A Petersburg game with a positive expected value would, assuming frictionless arbitrage, immediately go bust. Thus it will only survive on the margin as a Ponzi scheme or 'tax on stupidity' or a sort of cheap thrill indulged in occasionally.
Peters doesn't get this.
This seems to indicate that if individuals were willing to pay the highest price they
can afford, Menger would have considered his paradox resolved. Assuming that the
highest price one can afford is one’s entire wealth (i.e. that borrowing is impossible),
Menger’s statement that “no normal person would risk his total fortune” would mean
that by “risk” he meant “pay as a ticket price” and that he thought no one would pay
his total fortune for a ticket in his game B. But since the worst-case outcome is a gain
greater than the total initial fortune, there is no reason not to pay one’s total fortune.
Yes there is. Even if borrowing were disallowed, a coalition of buyers could immediately bankrupt the lottery. The fact that they haven't already done so means this is a 'tax on stupidity' or short run Ponzi scheme.
Peters himself notes-
Mathematical statements are correct in a sense that statements of other type are not. The
price we pay for the certainty inherent in mathematical statements is that they refer
to objects that don’t exist in an everyday sense of the word “exist”. It would be na¨ıve
to use any mathematical criterion as a guide for decisions without questioning the
criterion’s conceptual meaning and the axioms upon which its derivation rests. Applicability, or relevance to the real world, pertains only insofar as the axioms and their
consequences are a reflection of the real world.
This is quite foolish. Axioms may reflect the real world and still be useless. They may be unrealistic and yet make useful predictions.
Bernoulli and Menger and so on may have been wrong about why Petersburg lotteries are avoided- it is because the Expected value depends on the actions of all other potential customers, not on the proffer itself- but their being wrong didn't matter because they were writing shite for other shite pedagogues.
Peters, too is wrong for the same reason.
The ergodicity resolution... assumes that equivalent lotteries can be played arbitrarily often,
and this breaks down in Menger’s game – games of his type are atypical in the real
world. If we come across such a game, it is a once-in-a-lifetime opportunity.
Like getting Madoff to accept you as an investor.
Mathematics cannot offer much help in this situation.
But Economics can help. If a proffer has a positive expected value you need to look at the Structural Causal Model which permits this to happen. In other words, you've got to look at fundamentals, do due diligence, 'kick the tyres' and other such humdrum stuff. Writing equations and dreaming of infinite wealth may get you paid- but the guy cutting your checks is either a con-man or a cretin.
It makes sense of random events
only by embedding them in an ensemble of similar events, which may reside in parallel systems or within time.
Events occur in time. We have no access to 'parallel systems'.
In the single-event setup, mathematics must shrug its
shoulders and admit defeat in the face of a moral decision.
No. In a single-event set up, mathematics can look at the components of the Structural Causal Model which may involve Physics or Psychology or Organic Chemistry. Maths can make those disciplines more productive.
There is nothing wrong with the mathematics in the ergodicity resolution [Peters(2011)].
If we are really offered Menger-type games to be played at an arbitrarily high frequency, so that we can play arbitrarily often in our finite lives, then criterion ii will
be practically meaningful.
But it would be mischievous. We'd end up being suckered by a Madoff or made a laughing stock by a guy stupider than ourselves.
It is important to note that the time average growth rate
(or expected net change in logarithmic utility) in game B does not fail to resolve
Menger’s paradox mathematically (unlike the expectation value in the original game
A).
That's why we know it is a crock of shit. A mathematical formalism which explains why Jack should barter his cow for a handful of 'magic' beans' is worthless.
Elsewhere Peters writes-
One method of computing both ensemble and time averages is to write down
for a finite number of sample members and a finite sampling time an estimator of
the quantity of interest. One then considers two different limits: for the ensemble
average the number of samples is taken to infinity, and for the time average time is
taken to infinity. If the two limiting processes do not commute, then the ensemble
average is different from the time average, and the system is manifestly not ergodic
Economic processes do not correspond to ensembles- because of mimetic as well as 'Common Knowledge' type effects- which do not obtain in Physics. Nor are they usefully considered as 'time averages'. Essentially, a 'repeated game' equilibrium can be established very quickly but there is likely to be hedging on discoordination games so the dynamics becomes 'anything goes'.
Still, if at the margin, exogenous factors- not hysteresis- drive the dynamics, then we say the process is ergodic. Common Knowledge, 'Public signals' and mimetic effects can get rid of hysteresis very quickly though, it may be, the system preserves a 'memory' of this which is helpful for robustness or 'capacitance diversity'.
Some pedagogues may spell all this out and show it corresponds to Hannan consistent heuristics and links up with Evolutionarily Stable Strategies and some particular multiplicative update weighting algorithm and so on. But why bother? There is a demand for shite Economics and so sound-bite uttering Nobel laureates we shall always have with us as reminder of the ludic potential of the dismal science.
Peters, in his blog post, mentions 'prospect theory'- nudge, nudge, wink wink...
Especially in the context of prospect theory one often finds statements criticizing EUT that are puzzling. Like this one from the 2002 Nobel Prize Ceremony Speech:
“A key element in prospect theory is that individuals compare uncertain outcomes with a reference level which depends on the decision situation, instead of evaluating the outcome according to an absolute scale.”
EUT already includes such a reference level: initial wealth.
But we don't know what is or isn't wealth. That's where the Uncertainty comes in. Only time will tell which assets hold their value and which were worthless.
- Only under linear utility does the reference level cancel out. A researcher who assumes that Bernoulli and EUT are identical is likely to assume implicitly that utility is linear, in which case the reference level cancels out and would have to be re-introduced.
Who gives a shit about these 'researchers'? They ain't finding the cure to cancer are they? They might equally well be doing Post Colonial theory or Jungian basket-weaving.
- Kahneman refers directly to Bernoulli in his Nobel lecture, aware that something is not working in Bernoulli’s theory, but apparently unaware that Bernoulli’s theory is not the same as EUT.
So what? The guy was laughing all the way to the Bank.
- Let’s start considering time and ergodicity
Why? Will it make our dicks bigger?
Finally: a plea for treating the problem with the modern mathematical concepts we now have. By this, I mean: start worrying about time, and compute time-average growth rates.
Then travel back in time and give Bernie Madoff all your money. The maths shows he was right all along.
- The “expected change of logarithmic utility” is nothing but the time-average growth rate of wealth, under multiplicative dynamics.
But it is also utterly imbecilic nonsense.
- You can learn more about this in our lecture notes. Once this concept has sunk in — that gambles are evaluated according to the growth rates they generate for those who engage in them — the type of confusion that surrounds EUT becomes almost impossible.
Some gamblers do get rich. Some people do win the lottery. So what? It is still a tax on stupidity.
As for EUT- it has no place in the real world where Knightian Uncertainty obtains. 'Regret Minimization' dictates putting pressure on Regulatory Agencies to get Mechanism Design right. Also, it says enough with the Junk Social Science. Only Structural Causal Models which permit 'piecemeal engineering' deserve attention.
EUT is the foundation of modern economics.
Only from the point of view of pedagogues.
- Despite this, I have yet to find a practitioner who uses it.
Thus it isn't really the foundation of anything.
- Of course I may be exposed to an unusual sample, but in my experience investors, bankers, risk managers, gamblers — no one uses EUT. Shouldn’t that give us pause? Economics is devoted to the quantitative evaluation of risky prospects, but the people who quantitatively evaluate risky prospects for a living make no use of the techniques it has developed.
Economics is not the teaching of Economics anymore than Creative Writing is the teaching of Creative Writing.
- The fundamental and fatal flaw is conceptual — parallel universes are used where there should be time and dynamics.
It is because Time is not independent of Space that parallel universes popped up in Physics.
- Because of this flaw, there’s nothing to check against, the theory is not falsifiable because it depends on unobservable states of happiness or discomfort.
But Revealed Preferences are observable- coz they are revealed. Happiness is expressed. Discomfort gives rise to one's hopping from one foot to another in the queue for the toilet.
- Technical errors and inconsistencies can be argued away. It’s what Pauli called “not even wrong,” and the result of this murkiness is the coexistence of mutually exclusive, contradictory theories. Nothing is wrong and nothing is right. Different “schools of thought” have emerged. Let’s acknowledge that and ask what it means. This happens in science but it’s always a sign that a deep flaw has to be corrected, that the appropriate language has not been found yet.
This also happens in discussion about whether Spiderman can beat up Dracula. Even smart people let off steam by arguing about silly stuff. Academic methodenstreit was long ago discovered to be utterly useless. What matters is Structural Causal Models which enable us to have cool new stuff at a cheaper price.
We believe we now know that appropriate language. It’s the language of time and dynamics.
Languages exist only in time. They are already dynamic. Maths has a long way to go till it catches up with three year old kids in this respect. Till it does, it should not consider its dirty diapers to be any great contribution to the commonweal.









